Visual differential geometry and forms - 2

After solving the limit from the first part of Visual Differential Geometry and Forms: A Mathematical Drama in Five Acts by Tristan Needham, we can now move on to the next part. This is covering 2 out of the 3 chapters from the second act of the book, The Metric, plus the corresponding exercises.

Chapter 4: Mapping Surfaces: The Metric 🔗

The metric, which also used to be known as the first fundamental form, is a rule for the infinitesimal distance between neighboring points on a surface. This captures the essence of all possible surfaces having similar intrinsic geometry. The metric can help measure the length of any curve (integral), which can then be used to determine geodesics (shortest routes between two points), and then angles.

To determine this metric for a new surface \(\mathcal{S}\) we construct a function mapping every point \(\hat{z}\) from \(\mathcal{S}\) into a point \(z\) on the plane – let’s assume we work with the complex plane \(\mathbb{C}\). This is similar to trying to get a map of the world on a flat piece of paper, so we know it is impossible to not create distortions – because any triangle on the plane has excess angle \(\mathcal{E} = 0\) but on a general surface \(\mathcal{E} \ne 0\).

Consider two points \(\hat{z}\) and \(\hat{q}\) on the \(\mathcal{S}\) surface, infinitesimally close to one another. When we translate these points to the “map” (\(\mathbb{C}\)) we get point \(z = re^{i\theta}\) and \(q = z + dz\), respectively. On the complex plane, these points are separated by amount \(dz\), which is also a complex number. Thus, we can write \(dz = dse^{i\gamma}\) where \(ds\) is the length of this segment on the map and \(\gamma\) is the angle it makes with the \(Ox\) axis. The metric gives us an expression to relate the distance on \(\mathcal{S}\), \(d\hat{s}\) to \(dz\):

\[d\hat{s} = \Lambda\left(z,\gamma\right)ds\]

If \(\mathcal{S}\) is a sphere (actually, the southern hemisphere), we can construct the map to a plane using a projective map method: imagine the sphere is transparent and there is a light source in its center. Each light ray would hit both the sphere (point \(\hat{z}\)) and the plane (point \(z\)). A cone of light hits the sphere in a circle but the plane in an ellipse – and in general, for any surface \(\mathcal{S}\), the smaller the circle we consider to be mapping to the map, the closer its projection would be to an ellipse.

Hence, on the sphere we get

\[d\hat{s}^2 = \frac{R^2}{r^2+R^2} \left[\frac{R^2}{r^2+R^2}dr^2 + r^2d\theta^2\right]\]

or, if using latitude (\(\phi\)) and longitude (\(\theta\)) angles

\[d\hat{s}^2 = R^2\left[\sin^2\phi d\theta^2 + d\phi^2\right]\]

These two formulas, although they read differently, represent the same thing. This is similar to how on a plane one would compute an infinitesimal distance as \(ds^2 = dx^2 + dy^2\) if using Cartesian coordinates but as \(ds^2 = dr^2 + r^2d\theta^2\) if using polar coordinates.

To compute the metric in general, around a patch of the surface \(\mathcal{S}\), we start with the mapping process: we want to assign to every point \(\hat{z}\) on the surface a point \(z = u + iv\) in the complex plane¹. But how do we determine \(u\) and \(v\)? Well, we start by drawing a family of curves (called \(u\)-curves) such that at every point on the patch there will be exactly one line in this family that passes through it. We assign each curve in the family a number and require that these numbers can be varied smoothly – when moving from one curve in the family to another. For \(v\), we draw a similar family (\(v\)-curves), additionally requiring that no curve in the new family coincides with a curve in the \(u\)-family. This ensures that every point \(\hat z\) is uniquely identified as the intersection of an \(u\)-curve and a \(v\)-curve, so their corresponding numbers is what we use in the map as the values for \(z = u + iv\). Then, to compute the metric, we nudge the point \(\hat z\) by \(d\hat s_1\) along the \(v\)-curve and this results in a change \(du\) in the map. These changes are proportional if the nudge is infinitesimal and we define this proportionality constant to be \(A\). Similarly, we compute \(B\), the proportionality constant if we nudge the point \(\hat z\) by \(d\hat s_2\) along the \(u\)-curve, resulting in a change \(dv\) in the map.

\[\begin{align} A &= \frac{d\hat s_1}{du}\\ B &= \frac{d\hat s_2}{dv}\\ \end{align}\]

In general, the \(u\) and \(v\) curves are not orthogonal, let’s denote their angle by \(\omega\). As shown below, we have the following nudges:

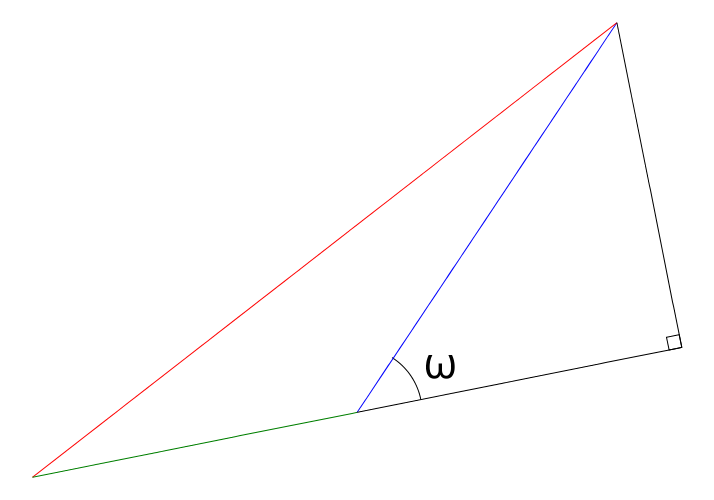
where \(d\hat s\) is represented in red, \(d\hat s_1\) in green and \(d\hat s_2\) in blue. Unfortunately, the system I’m using for diagraming does not support all Unicode characters, nor does it support LaTeX. I will have to fix this in a separate article.

Coming back to the topic, now we can compute the value of \(d\hat s^2\):

\[d\hat s^2 = A^2du^2 + 2AB\cos \omega dudv + B^2dv^2\]

where we can use \(F = AB \cos\omega\). This is the metric formula.

One question that arises is how can we use this to determine the curvature, \(\mathcal{K}\)? There is this formula which will be proven later:

\[\mathcal{K} = - \frac{1}{AB} \left(\partial_v\left[\frac{\partial_v{A}}{B}\right]+\partial_u\left[\frac{\partial_u{B}}{A}\right]\right)\]

Similarly, one element of infinitesimal area is given by

\[d\mathcal{A} = \sqrt{\left(AB\right)^2-F^2}dudv\]

Next, we are introduced to the concept of conformal maps. Here, we sacrifice straight lines to guarantee that angles between two curves are also preserved (in magnitude) on the flat map. If the angle orientation change then we have anticonformal maps.

For these maps and for these maps alone, the expansion factor \(\Lambda\) does not depend on the direction \(\gamma\). Then circles will always be mapped to circles, \(A = B = \Lambda\) and

\[d\hat s^2 = \Lambda^2\left[du^2+dv^2\right]\]

This makes curvature formula be more elegant, by using the second order Laplacian operator \(\nabla^2 \equiv \partial_u^2 + \partial_v^2\):

\[\mathcal{K} = -\frac{\nabla^2\ln\Lambda}{\Lambda^2}\]

Every surface has an infinite variety of conformal maps. The coordinates are also called isothermal coordinates. This is because we can replace any complex number \(z\) by a number \(ae^{i\tau}z+w\) (that is, scale the entire complex plane by \(a\), rotate by \(\tau\) and translate by \(w\)) and then compose this transformation with the conformal mapping to obtain another one. In fact, any analytical function can be used here (where \(a\) and \(\tau\) now depend on the value of \(z\)).

This fact allows us to define conformal mappings from \(\mathcal{S}\) back to \(\mathcal{S}\) itself by using composition! If we have a conformal map \(F : \mathbb{C}\rightarrow\mathcal{S}\) and an analytic function \(f : \mathbb{C} \rightarrow\mathbb{C}\) then \(F\circ f\circ F^{-1}\) is a conformal mapping from \(\mathcal{S}\) to \(\mathcal{S}\).

So, what is a conformal map of a sphere? This is the stereographic projection: instead of having the light source in the center of the sphere as before, place it at the north pole and place the plane at the sphere’s equator (keeping it tangent to the south pole only introduces a factor of \(2\)). If the sphere has radius \(1\), we obtain the Riemann sphere. If we add a point at infinity to represent the north pole (the only one who doesn’t have a shadow on the plane), we get the extended complex plane.

In this case, we have:

\[d\hat s^2 = \frac{2R^2}{R^2+r^2}ds^2\]

Using the Laplacian in polar coordinates, \(\nabla^2 \equiv \partial_r^2 + \frac{1}{r}\partial_r + \frac{1}{r^2}\partial_\theta^2\) we recover that the curvate is \(\mathcal{K} = \frac{1}{R^2}\).

The chapter then continues to derive transformations on the stereographic projection on the unit sphere between points on the plane and points on the sphere, using either cartesian coordinates (\(\hat z\) given by \((X, Y, Z)\), \(z = x + iy\)) or polar coordinates (\(\hat z\) given by angles \((\phi, \theta)\) – where \(\phi\) measures angle from north pole, the reverse of what we’d consider a latitude angle –, \(z = re^{i\theta}\)):

\[\begin{align} x + iy &= \frac{X+iY}{1-Z}\\ X+iY &= \frac{2z}{\left|z^2\right| + 1}\\ Z &= \frac{\left|z^2\right| - 1}{\left|z^2\right| + 1}\\ z &= \cot\left(\frac{\phi}{2}\right)e^{i\theta} \end{align}\]

From these, we can prove that if we have \(p\) to be the projection of \(\hat p\), then we can find \(q\) the projection of \(\hat q\) by:

\[q = -\frac{1}{\overline{p}}\]

We also obtain that any circle not passing through the north pole is projected back into a circle on the stereographic plane.

Chapter 5: The Pseudosphere and the Hyperbolic Plane 🔗

The chapter starts by a little piece of history about hyperbolic geometry and how to make it real it needed a surface of constant negative curvature. We’ve already seen it, but this chapter defines it properly: the pseudosphere.

The pseudosphere is defined as the rotation of a curve around an axis. The curve is called the tractrix, it is generated by attaching a piece of string to an object on a table and then pulling the string along a certain axis. The trajectory of the object describes the tractrix – I had a post on the old blog about a very similar curve which I might modernize and bring up here in the future.

If the length of the string is \(R\), the we can determine the distance \(X\) between the object and the rotation axis as \(X = Re^{-\sigma/R}\) where \(\sigma\) represents the length of the curve that the object already traveled. This can be used to determine the metric \(d\hat s^2\) and then the curvature \(\mathcal{K}\) which would be \(-\frac{1}{R^2}\) always.

There are 2 problems with doing geometry directly on the pseudosphere. First, because it is a rotation surface, it is more akin to a cylinder than to a plane: moving around a certain line would return you to where you started. Worse, some line segments cannot be extended infinitely in both directions: we have a rim – which is essential for surfaces with constant negative curvatures – and we cannot go past it.

However, we can construct a conformal map that solves these problems at the same time. For now, let’s use \(x\) to denote the rotation angle. On the surface, on a circle parallel to the rim, with radius \(X\) (from above \(X = Re^{-\sigma/R}\)), a small nudge of this angle by \(dx\) results in a nudge of \(Xdx\). But on the map it would only be \(dx\), so we have a shrink factor of \(1/X\). This must apply in any direction around that point (because we have a conformal map) and this forces us to pick \(y\) that satisfies

\[\frac{dy}{d\sigma} = \frac{1}{X} = \frac{e^{\sigma/R}}{R}\]

From this, integrating and setting the constant to 0 we have

\[y = e^{\sigma/R} = \frac{R}{X}\]

and the metric is

\[d\hat s = Xds = \frac{R\sqrt{dx^2+dy^2}}{y}\]

From this, an area \(dxdy\) on the map is related to the true area \(d\mathcal{A}\) on the pseudosphere by

\[d\mathcal{A} = \frac{R^2}{y^2} dx dy\]

This means that circles of the same area on the surface will appear larger and larger in the conformal map the higher we move along the surface (that is, the farther from the rim we go).

This is a conformal map, but it doesn’t solve our problems. It is only defined on the \(\{(x, y) | 0 \le x \lt 2\pi, y \ge 1\}\) subset of the complex plane – it is a rimmed cylinder. We can remove the bounds on \(x\) by periodicity and the bound on \(y\) by replacing it with 0, as long as we keep the \(1/y\) factor in the metric – we cannot go below 0, here Zeno’s paradox is real.

Thus, we arrive at the hyperbolic plane, \(\mathbb{H}^2\): the entire half-plane \(y \gt 0\) with metric \(d\hat s=\frac{ds}{y}\). Points on the line \(y = 0\) are points at infinity, or ideal points and the line itself is called the horizon.

The shape of this metric means that particles that move with constant speed on the pseudosphere will move with a speed that is equal to \(y\) on \(\mathbb{H}^2\). Coupling this with Snell’s law (from optics) results that geodesics in the hyperbolic plane satisfy \(\sin\theta/y = constant\), they are semicircles with the center of the line \(y=0\). Since we can construct multiple circles that pass through the same point \(p\) (see figure below), but not all of them will intersect another fixed semicircle (the blue semicircle), we get that we can build more than one (ultra-)parallels to a line \(L\) from a point \(p\)!

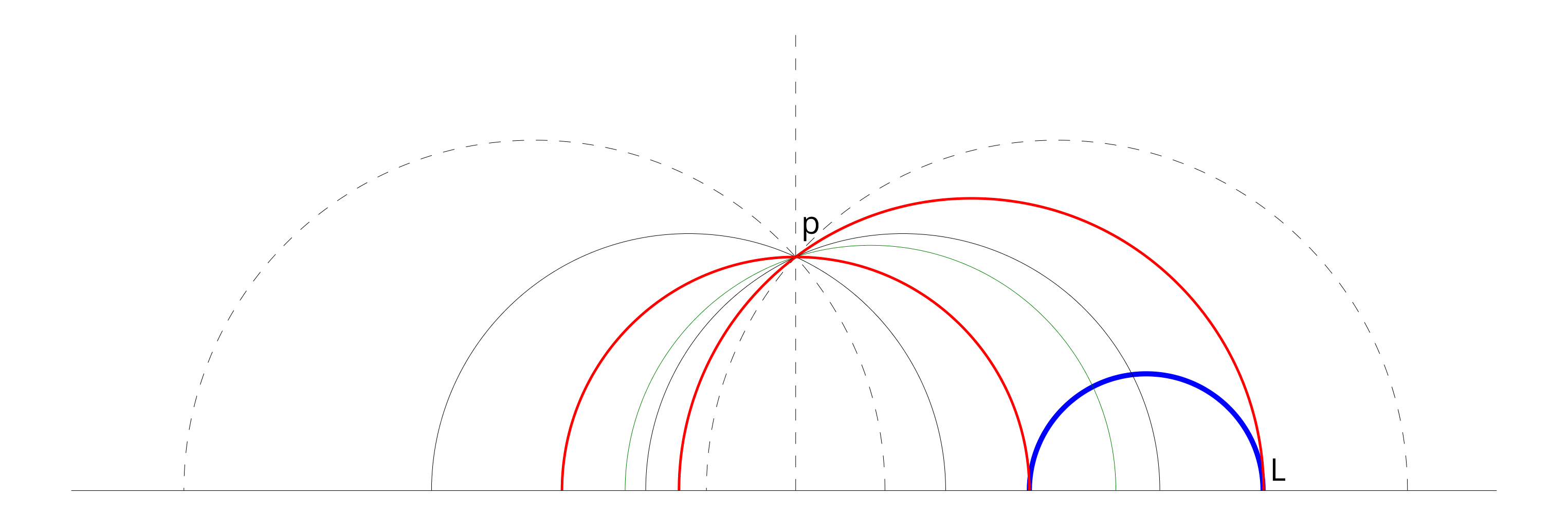
In this image, all ultra-parallels are dashed. There is a particular one that is a vertical line instead of a semicircle, but for someone living on the geometry it will still look like any other semicircle, it’s just that the radius is infinite. All non dashed lines intersect \(L\), but there are 2 special types of lines: the 2 red ones are asymptotics, they are tangential to the semicircle that corresponds to \(L\). The green one is orthogonal to \(L\), it intersects it at a right angle. This will become useful soon.

One interesting thing we can do on the hyperbolic plane is to rotate it around our point \(p\) of interest. For each angle of rotation, some lines that were semicircles now become vertical lines – a semicircle with infinite radius. So, we can perform this transformation – a particular case of an isometry – until the line \(L\) we want to draw a parallel to becomes vertical, such as in the following image:

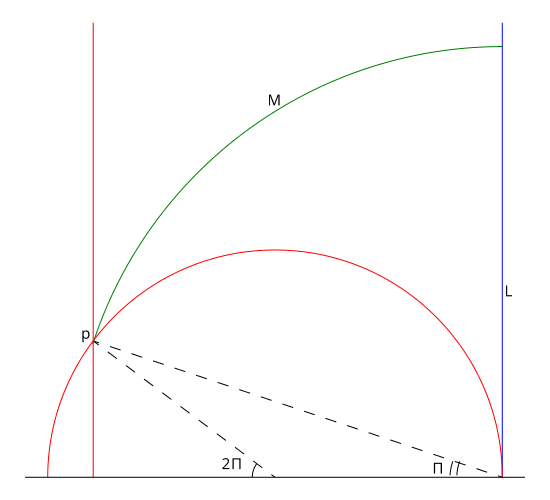
One of two semicircles that were tangent to \(L\) – the asymptotics – also became a vertical line – reasoning left as an exercise to the reader. Looking at the line \(M\) that is perpendicular to \(L\) (the green line in the two figures) we can determine this relationship between the angle \(\Pi\) (half of the angle between the asymptotics, the angle between \(M\) and each one of them) and the distance \(D\) (measured on \(M\), the shortest distance) between \(p\) and \(L\):

\[\tan\left(\frac{\Pi}{2}\right) = e^{-D}\]

Another conformal map for the hyperbolic plane is the Beltrami-Poincaré disk: the horizon is represented by the unit circle, geodesics are circular arcs that meet the horizon at right angles, as shown below:

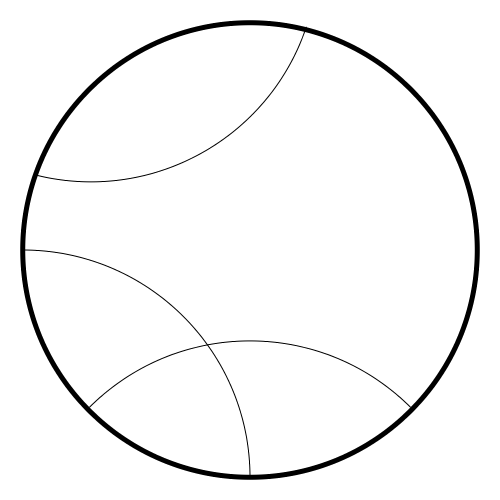
If \(r\) is the distance from the center of the disk, then the metric is given by:

\[d\hat s=\frac{2}{1-r^2}ds\]

There is a simple transformation between these two models, as we will see later in the exercises chapter. For now, we can enjoy the fact that we have built 2 non-Euclidean geometries with constant curvatures: one on the sphere (positive curvature) and one on the pseudosphere, modeled via the Beltrami-Poincaré semiplane or the Beltrami-Poincaré disk (negative curvature). We have ways to measure distances, angles and areas on all such surfaces (and many others), starting from just a single formula, the metric.

There is one more chapter in this part of the book, but I will push it for the next session of this blog series as this one is already long. So, we will skip to:

Chapter 7: Exercises for Act II 🔗

This chapter has exercises for chapters 4, 5, and 6. However, we only went through the first two of these, so we will only discuss the interesting exercises pertaining to those chapters.

The first interesting exercise is number 8, which involves certain algebra and calculus to prove that if we have a general metric

\[d\hat s^2 = A^2du^2 + 2Fdudv + B^2dv^2\]

then we can find new coordinates \(U\) and \(V\) which are conformal. These are two simultaneous solutions to the Beltrami-Laplace equation:

\[\partial_v\left[\frac{A^2\partial_v\Phi-F\partial_u\Phi}{M}\right] + \partial_u\left[\frac{B^2\partial_u\Phi-F\partial_v\Phi}{M}\right]= 0\]

where we use \(M = \sqrt{\left(AB\right)^2-F^2}\) and \(\Phi\) is the unknown function we have to solve for. If the original metric was already conformal, this reduces to the Laplace equation:

\[\partial_x^2\Phi + \partial_y^2\Phi= 0\]

Then, exercises 10, 11, and 12, discuss 3 different projections from the sphere to a flat plane: the Archimedes-Lambert projection on a cylinder, the central cylindrical projection (same setup but projecting lines all start from the center of the sphere) and the Mercator projection (which is conformal). Finally, exercise 13 asks if there is a map that can preserve both areas and angles and we already have a negative answer to that.

Moving to the exercises for the next chapter, in 15 we have to prove that the geodesics in the \((x,y)\)-plane with \(v = 1/\sqrt{1-y}\) are parabolas (by following the Snell’s law proof). In 16 we parameterize the tractrix and the pseudosphere using cylindrical polar coordinates and then we use the same coordinates in exercise 17 to compute areas on a sphere. Finally, in exercise 18 we prove that the pseudosphere has finite area despite the fact that it is unbounded.

Finally, exercise 22 involves surfaces of revolution that have constant curvature, generalizing on the sphere and the pseudosphere. Then, exercise 23 discusses the torus and asks us to prove that the total curvature on the entire torus vanishes.

With this, we finish the second reading session on VDGF. The last few articles have been math heavy, so I am planning to take a break from this and do some pure programming for the next installment.