About that limit from VDGF

In the last section of a previous article I presented a limit that was given as an exercise in Visual Differential Geometry and Forms: A Mathematical Drama in Five Acts by Tristan Needham. In the last article I set up the needed infrastructure to solve it in this post. So, let’s solve it now.

To reiterate, we need to determine the value of the following:

\[\lim_{x \rightarrow 0}{\frac{\sin\tan{x} - \tan\sin{x}}{\sin^{-1}\tan^{-1}{x} - \tan^{-1}\sin^{-1}{x}}}\]

I will go over multiple avenues, it might look complicated. But, there is a very simple solution to this problem. If you don’t want to go over the entire article, jump directly to the simple solution section.

Calculus and algebra 🔗

We know that \(\sin{0} = 0\) and \(\tan{0} = 0\) so it becomes evident that the limit is a case of \(\frac{0}{0}\). Naively, one might think of applying the l’Hopital rule. But a quick attempt at computing the first derivatives of the terms in the numerator already hints that this would be a Sisyphean task:

\[\begin{align} \frac{d\sin{\tan{x}}}{dx} &= \frac{\cos{\tan{x}}}{\cos^2{x}}\\ \frac{d\tan{\sin{x}}}{dx} &= \frac{\cos{x}}{\cos^2{\sin{x}}} \end{align}\]

In fact, by also taking the approximations that \(\sin{x} \asymp x\) and \(\tan{x} \asymp x\) we can glimpse that the first derivative would still result in a numerator of \(0\), meaning that we might even need to compute the second derivatives of these functions too! Or maybe even more – as we will see later.

Turning to ChatGPT or Bard is of no use. While operating with the above complicated expressions (or similar), both of these AI start dropping trig functions, transforming, for example, \(\cos\sin x\) into \(\cos x\) and then reaching wrong answers. WolframAlpha computes the limit to be \(1\), but this is definitely cheating, we won’t learn anything by just using it.

The next approach would be to try and compute Taylor series around 0 until we find terms that are not equal (guaranteed, since \(\sin\tan x \ne \tan\sin x\) in general). However, computing these Taylor series directly results in computing the same derivatives as before, so still a large amount of work.

Simplify and conquer via algebra 🔗

Instead, let’s look at the pattern of the limit. If we denote by \(f(x) = \sin\tan x\) and \(g(x) = \tan\sin x\) then the limit is now:

\[\lim_{x \rightarrow 0}{\frac{f(x) - g(x)}{g^{-1}(x) - f^{-1}(x)}}\]

This hints that we could halve the work we need to do if we can find a relationship between the Taylor series of \(f^{-1}\) (or \(g^{-1}\)) and \(f\) (or \(g\)). We could compute the coefficients of the direct function (using the large amount of work that involves computing all those derivatives mentioned above) and then follow an algorithm to determine the coefficients of the function’s inverse.

Fortunately, such an algorithm exists, under some conditions, because there is a relationship between a function and its inverse: composing them must result in the identity function. That is:

\[\begin{align} f(f^{-1}(x)) &= x\\ f(f^{-1}(x)) &= x \end{align}\]

Suppose we have a nice function \(f\) such that we can write both \(f\) and its inverse using Taylor expansions around 0 – for some coefficients:

\[\begin{align} f(x) &= a_0 + a_1x+a_2x^2 + \ldots &= \sum_{i=0}^\infty{a_ix^i}\\ f^{-1}(x) &= A_0 + A_1x+A_2x^2 + \ldots &= \sum_{i=0}^\infty{A_ix^i} \end{align}\]

We only care if these series converge around 0 since that’s where we want to compute the limit at. This means we can also truncate the series to only a finite number of coefficients. If we can compute each \(A_i\) from this finite set using only the finite set of \(a_j\) values then we have our algorithm.

To start with, suppose we use a very narrow interval where we can approximate each function by a linear term (assuming \(a_1 \ne 0\) and \(A_1 \ne 0\)). That is,

\[\begin{align} f(x) &= a_0 + a_1x\\ f^{-1}(x) &= A_0 + A_1x \end{align}\]

In this case, we have the following

\[\begin{align} f(f^{-1}(x)) &\asymp a_0 + a_1f^{-1}(x)\\ &\asymp a_0 + a_1\left(A_0 + A_1x\right)\\ &= \left(a_0 + a_1A_0\right) + a_1A_1x \end{align}\]

Since this must equal \(x\) we have

\[\begin{align} a_0 + a_1A_0 &= 0\\ a_1A_1 &= 1 \end{align}\]

That is,

\[\begin{align} A_0 &= \frac{-a_0}{a_1}\\ A_1 &= \frac{1}{a_1} \end{align}\]

This was trivial, so let’s look at the second order terms:

\[\begin{align} f(x) &= a_0 + a_1x + a_2x^2\\ f^{-1}(x) &= A_0 + A_1x + A_2x^2 \end{align}\]

From this, we have:

\[\begin{align} f(f^{-1}(x)) &\asymp a_0 + a_1f^{-1}(x) + a_2\left(f^{-1}(x)\right)^2\\ &\asymp a_0 + a_1\left(A_0 + A_1x + A_2x^2\right) + a_2\left(A_0 + A_1x + A_2x^2\right)^2 \end{align}\]

This becomes more convoluted, but we only care about terms raised to at most power of 2. So, when we expand we can ignore anything higher. By requiring the expansion to be identical to \(x\), we get:

\[\begin{align} a_0 + a_1A_0 + a_2A_0^2&= 0\\ a_1A_1 + 2a_2A_0A_1 &= 1\\ a_1A_2 + a_2A_1^2 &= 0 \end{align}\]

From the first equation we can determine \(A_0\) by using the quadratic formula. Replacing in the second one gives \(A_1\) and then we get \(A_2\) from the last equation. This is not much harder than when we stopped at the first term, we only have one quadratic equation and all the others are linear.

But, can we continue this process to determine all the needed \(A_i\) values? If we cannot do this, then we’ll be back to the drawing board, we need to find another approach. Fortunately, this works: in the Taylor expansion of \(f(f^{-1}(x))\) each \(A_i\) first shows up in the multiplier for \(x^i\). Thus, if we want to compute \(n\) coefficients of the Taylor expansion of the reverse function we only need to compute \(n\) coefficients of the original function, expand \(f(f^{-1}(x))\) and then solve the system of \(n\) equation that results when we consider multipliers for each power of \(x\). For \(A_0\) we have a equation of order \(n\), as we get one term from each multiplier of \(x^i\). However, each other term will be solved by a linear equation. Remember this point, as we will revisit it later.

Continuing on this plan of action, if we don’t want to build this system of \(n\) equations, we can use a theorem that gives the coefficients directly but this is a lot of work anyway.

This leads us to another question: how many coefficients do we need to compute to determine the value of the limit?.

Symmetry based simplification 🔗

Instead of answering that question, let’s see if we can exploit more of the problem formulation to reduce the amount of work. Consider again \(f\) and \(g\) from the limit:

\[\begin{align} f(x) &= \sin\tan x\\ g(x) &= \tan\sin x \end{align}\]

What if we simplify further? Consider \(u(x) = \sin x\) and \(v(x) = \tan x\). Then \(f = u \circ v\) and \(g = v \circ u\), just function composition where the \(u\) and \(v\) functions are placed in symmetrical positions. Thus, our limit becomes:

\[\lim_{x \rightarrow 0}{\frac{\left(u \circ v\right)(x) - \left(v \circ u\right)(x)}{\left(u^{-1} \circ v^{-1}\right)(x) - \left(v^{-1} \circ u^{-1}\right)(x)}}\]

Although this look more complicated, it helps us in determining how many terms in the Taylor expansion to compute. We can start with the Taylor expansions for \(\sin\) and \(\tan\), get an expansion for \(f\) and \(g\) and for their difference. We then pick the first coefficient that is not 0 and then follow the process from the previous section to determine the coefficients for the Taylor expansions in the denominator. Sounds like a plan, but wait, we can do even less work!

Both \(\sin\) and \(\tan\) have an additional symmetry that we can exploit: they are both odd functions. This means their Taylor expansion only contains terms in \(x^k\) where \(k\) is an odd number. It also means that their composition is an odd function, that is it only contains odd powers too. Can we determine these coefficients from the Taylor function coefficients?

Let’s assume that

\[\begin{align} u(x) &= d_1x + d_3x^3 + d_5x^5 + d_7x^7 + \ldots\\ v(x) &= c_1x + c_3x^3 + c_5x^5 + c_7x^7 + \ldots \end{align}\]

If we stop at the linear term, we have:

\[u(v(x)) \asymp d_1 c_1 x\]

This is a symmetric term, so it will be the same in \(v(u(x))\). Hence the difference would be 0, we still get in a \(\frac{0}{0}\) limit case.

Going to the cubic term we have

\[u(v(x)) \asymp d_1 c_1 x + (d_1c_3 + d_3c_1)x^3\]

This is still symmetrical, let’s go to the 5th power term:

\[u(v(x)) \asymp d_1 c_1 x + \left(d_1c_3 + d_3c_1\right)x^3 + \left(d_1c_5 + 3d_3c_1^2c_3 + d_5c_1\right)x^5\]

This is no longer symmetrical, exchanging all \(d\)s with \(c\)s would result in a different expression. So in this case \(u(v(x)) - v(u(x))\) will have a non-zero multiple of \(x^5\). But will this help in our case?

Turns out that for our limit we need to go one extra step. This is because:

\[\begin{align} \sin x &\asymp x - \frac{x^3}{6} + \frac{x^5}{120}\\ \tan x &\asymp x + \frac{x^3}{3} + \frac{2x^5}{15} \end{align}\]

That is, \(d_1 = c_1 = 1\) and the expression we got to is still symmetrical. Hence, let’s go to the 7th power term. Now:

\[u(v(x)) \asymp x + \left(c_3 + d_3\right)x^3 + \left(c_5 + 3d_3c_3 + d_5\right)x^5 + \left(c_7 + 3d_3c_5 + 3d_3c_3^2 + 5d_5c_3 + d_7\right)x^7\]

This time the multiplier of \(x^7\) is not symmetric. So now when we compute the difference we get:

\[u(v(x)) - v(u(x)) \asymp \left(2\left(d_5c_3-d_3c_5\right) + 3d_3c_3\left(c_3-d_3)\right)\right)x^7\]

If we replace the expressions for \(u = \sin\) and \(v = \tan\) we get:

\[\sin\tan x - \tan\sin x \asymp -\frac{x^7}{30}\]

What does this mean? We now know that we need to compute up to the 7th derivatives for all involved terms (though we only need half of them due to the functions being odd). We also know that \(\sin\tan x \le \tan\sin x\) on a small interval \((0, \alpha)\) before the \(x^9\) term becomes relevant.

Now, we can finally compute the limit.

Computing the limit, algebraically 🔗

Now that our detour to determine how many derivatives to compute is over, we can return to the scheme from two sections ago. We know that we need to express \(f\) and \(g\) up to the 7th order Taylor expansion and then we can compute the coefficients \(A_i\) for their inverses. That is, for each function, we need 8 coefficients, so a total of 28 values to compute?

Well, not so fast. We know that the functions are all odd and this halves the number of the terms in the expansion. We also know that the first derivative of both \(f\) and \(g\) is 1. So we only need to compute \(a_3\), \(a_5\) and \(a_7\) via derivatives and \(A_3\), \(A_5\) and \(A_7\) via the process described above (twice, once for \(f\) and once for \(g\)). Only 12 values. Should we start?

Well, let’s think a little bit more. We saw that all coefficients in \(f - g\) up to the 7th order cancel out. Do we get a similar thing for the coefficients in \(g^{-1} - f^{-1}\)?

If you remember the process to compute each \(A_i\), only \(A_0\) was the involved in a nonlinear equation. Fortunately for us, \(A_0 = 0\) (for both \(f\) and \(g\)), so we only have linear equations. But this means we can also write each \(A_i\) as a linear combination of \(a_1, a_2, \ldots a_i\) (where \(A_1, A_2, \ldots A_{i-1}\) can show up as coefficients of the linear expression).

But we also know that for our limit \(a_1 = A_1 = 1\). This mean – exercise left for the reader, you can prove it by induction –, that each \(A_i\) can be written as \(A_i = -a_i + P_i(a_2, a_3, \ldots, a_{i-1})\) where \(P_i\) is the linear combination that results from solving the corresponding system of equation.

In particular, if \(f\) and \(g\) share the first few coefficients (as we’ve seen \(a_1 = b_1 = 1\), \(a_3 = b_3\) and \(a_5=b_5\) and all others up to 7th order are 0), then their inverses will also share the same coefficients. Hence, the only one that are relevant are \(a_7\), \(b_7\), \(A_7\) and \(B_7\). The limit thus becomes:

\[\frac{a_7 - b_7}{B_7 - A_7} = \frac{a_7 - b_7}{a_7 - b_7} = 1\]

This is because the same polynomial \(P_7\) shows up in both \(B_7 = -b_7 + P_7\) and in \(A_7 = a_7 + P_7\) and all coefficients are equal.

So, we ended up computing the limit without needing to compute any derivatives, but only looking at the symmetry relations involved. We still needed to do a lot of algebra to prove some helper lemmas (which are useful in other similar cases). Isn’t there a faster approach?

Computing via geometry 🔗

The limit was given as an example that geometrical reasoning can be faster than algebraic manipulation. So, we need to solve it via geometry. We know that our functions \(f(x) = \sin\tan(x)\) and \(g(x) = \tan\sin(x)\) are 0 at 0 and have a derivative of \(1\). So, let’s plot \(f\), \(g\) and their inverses in the region where they are linear (and exaggerating the slopes):

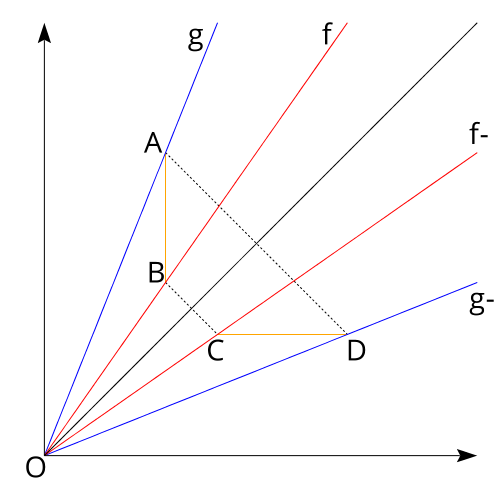
This diagram occurs because \(f \le g\) (proven at the end of two sections ago) and \(x \le f(x)\) (trivial to prove). The black diagonal marks the line \(y = x\), the blue lines are \(g\) and \(g^{-1}\), the red ones are \(f\) and \(f^{-1}\). Due to the definition of a function’s inverse the diagram is symmetrical across the diagonal line.

We just need to compute the ratio of the lengths of \(AB\) and \(CD\) as they get closer to the origin. Due to symmetry, these two segments are actually equal. Hence, the limit is \(1\).

The same proof would produce a similar result if \(f\) and \(g\) would be on different sides of \(y = x\).

Conclusion 🔗

We have proven that if we have two odd functions \(u\) and \(v\) such that their derivatives at 0 is 1 and \(u \circ v \ne v \circ u\) then the limit